Extracting arbitrary distributions from the model using vmc

Introduction

This vignette describes how to use the vmc package to define how to extract a data frame to use in model checks (e.g., tidy data frame) from arbitrary distributions that directly describe the model predictions (e.g., posterior predictive distribution) or indirectly describe the predictions via push-forward transformations (e.g., model variables like mu and sigma in Gaussian family models). For a more general introduction to vmc and its use on a standard model check workflow, see vignette("vmc").

Setup

The following libraries are required to run this vignette:

These options help Stan run faster:

rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

Bayesian models

vmc package uses the extraction functions from tidybayes package, which can work for the Bayesian models supporting fit and prediction, such as brms::brm() models and rstanarm``](https://mc-stan.org/rstanarm/reference/rstanarm-package.html) models. For a full list of supported models bytidybayesextraction functions, see [tidybayes::tidybayes-models`.

We go through this section using a built-in model mpg_model, a brmsfit object fitted in the Gaussian model family with push-forward transformations mu and sigma. The usage of other models is the same as long as they are supported by the extraction functions from tidybayes.

mpg_model
#>  Family: gaussian 
#>   Links: mu = identity; sigma = log 
#> Formula: mpg ~ disp + vs + am 
#>          sigma ~ vs + am
#>    Data: mtcars (Number of observations: 32) 
#>   Draws: 4 chains, each with iter = 6000; warmup = 3000; thin = 1;
#>          total post-warmup draws = 12000
#> 
#> Regression Coefficients:
#>                 Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept          23.25      2.87    17.57    28.92 1.00     6198     6420
#> sigma_Intercept     0.87      0.20     0.50     1.30 1.00    10336     7471
#> disp               -0.02      0.01    -0.04    -0.01 1.00     6404     6672
#> vs                  2.74      1.74    -0.73     6.14 1.00     6770     6991
#> am                  2.74      1.81    -0.76     6.36 1.00     6100     7119
#> sigma_vs            0.27      0.34    -0.38     0.95 1.00     6544     7801
#> sigma_am            0.34      0.36    -0.38     1.03 1.00     6925     7174
#> 
#> Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

Predictive distribution

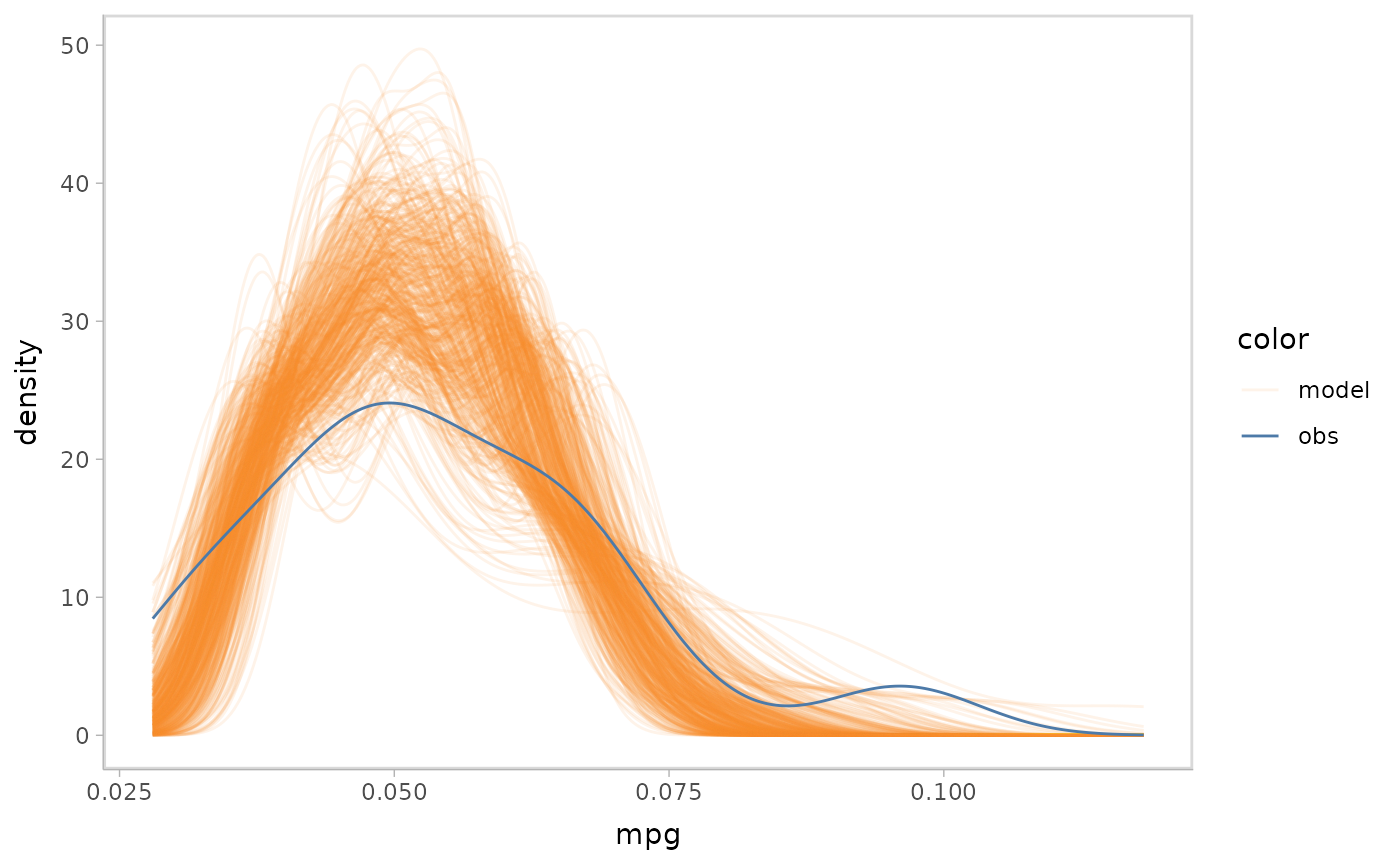
Now we have the data ready for doing model check. We could use a single mcplot() statement to generate a density plot for predictive distributions, where vmc uses tidybayes::predicted_draw() to extract tidy data frames from the model and then compares it with the observed data that uses to fit the model.

mpg_model %>%
  mcplot()
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.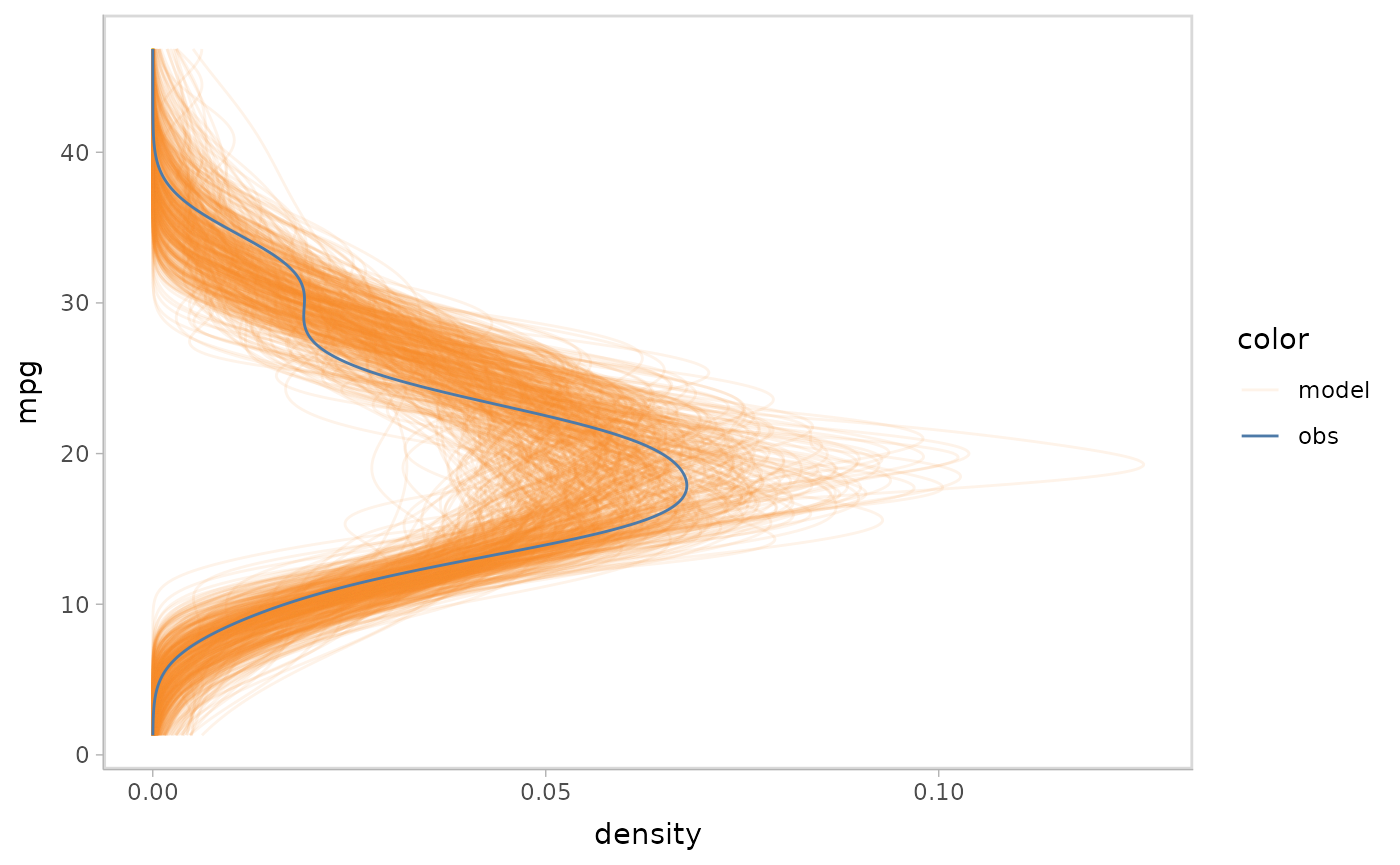

vmc puts the response variable on the y axis by default. We could use ggplot2::coord_flip() to flip the axes.

mpg_model %>%
  mcplot() +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.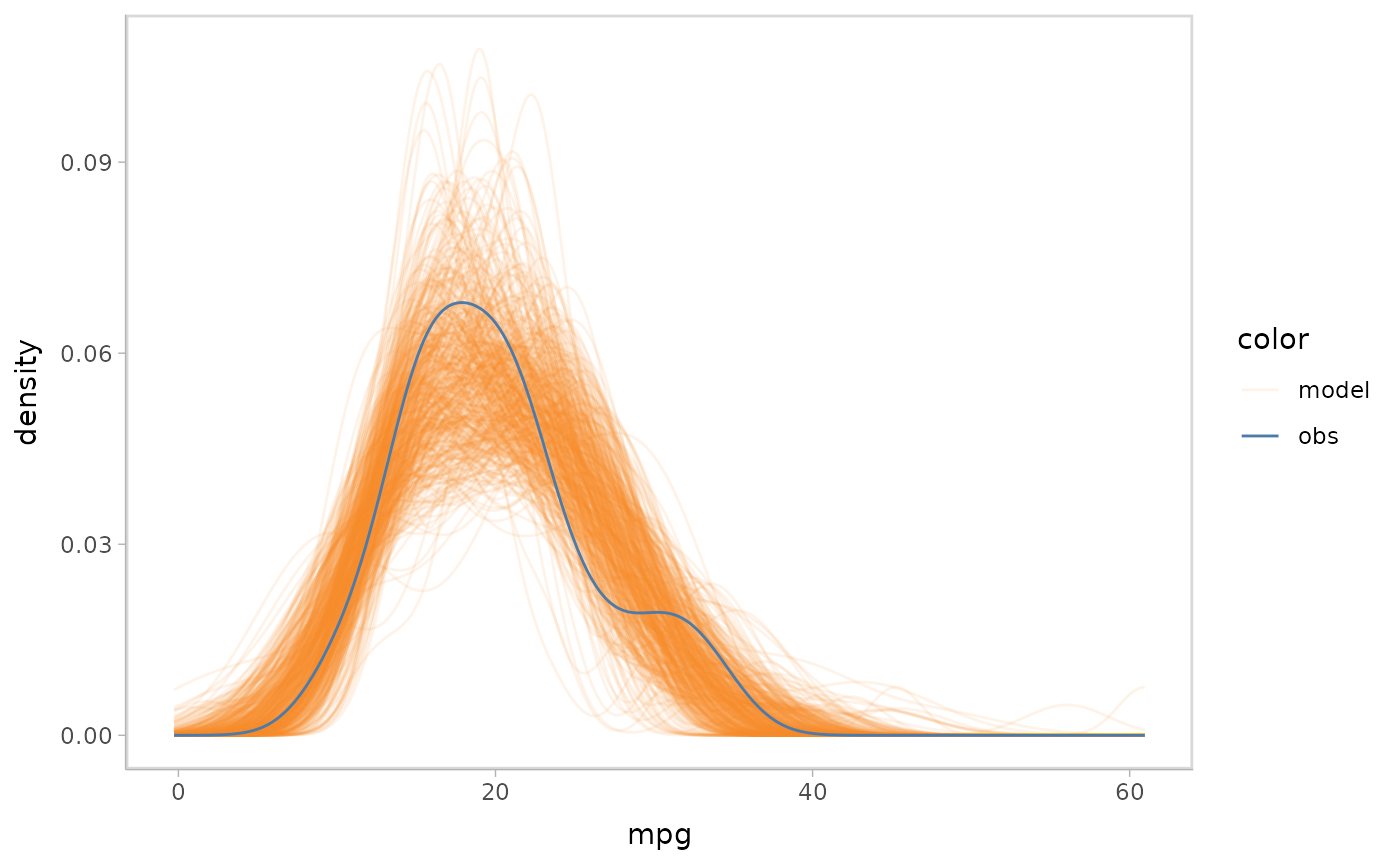

Push-forward transformations

Only checking the predictive distributions might not fulfill all the purposes of model check. Imagine a scenario where the model designer identifies misalignment between the model predictions and observed data. This may lead them to want to know more details about which part of the model leads it to behave differently from the observed data. For a Bayesian model, they can access those quantities by extracting push-forward transformations. For example, when they find a mismatched pattern in a Gaussian predictive model, they can check whether the mean of the model mismatches, the variance of the model mismatches, or whether both mismatch by checking the mu push-forward transformation and the sigma push-forward transformation separately. After identifying which part is more responsible for they discrepancy, they can correct that part in the formula of the model or change the prior to better align predictions with the observed data.

mpg_model %>%
  mcplot() +
  mc_draw("mu") +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.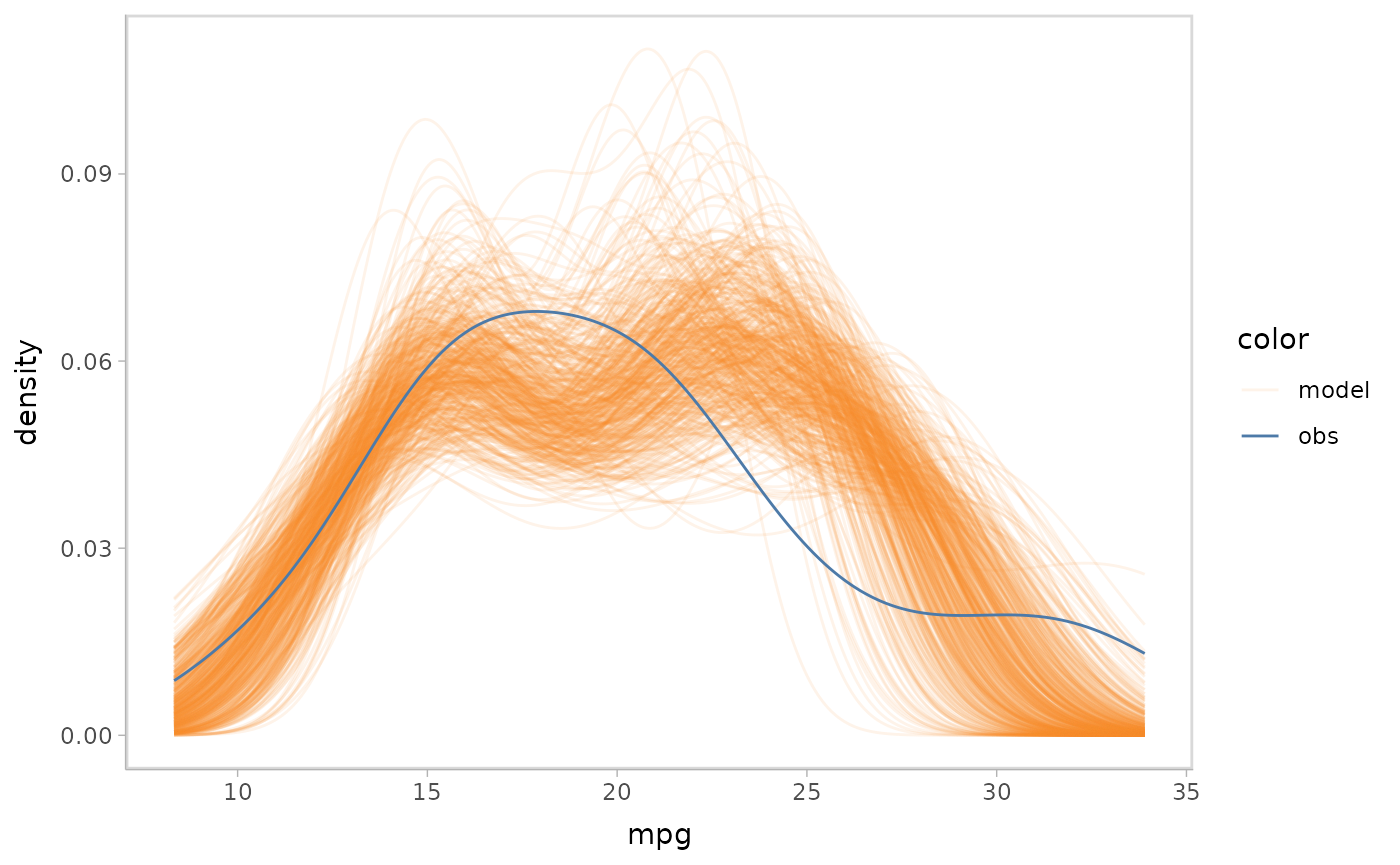

Some model variables have a different unit than the observations of the response variable, such as sigma in a Gaussian model, which will make them incomparable. In that case, we could add a transform function for the observed data to bring them into the same unit. For example, the sigma push-forward transformation describes the variance of the observed data, so we could transform the observed data using sd().

mpg_model %>%
  mcplot() +
  mc_observation_transformation(sd, vars(vs, am)) +
  mc_draw("sigma") +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.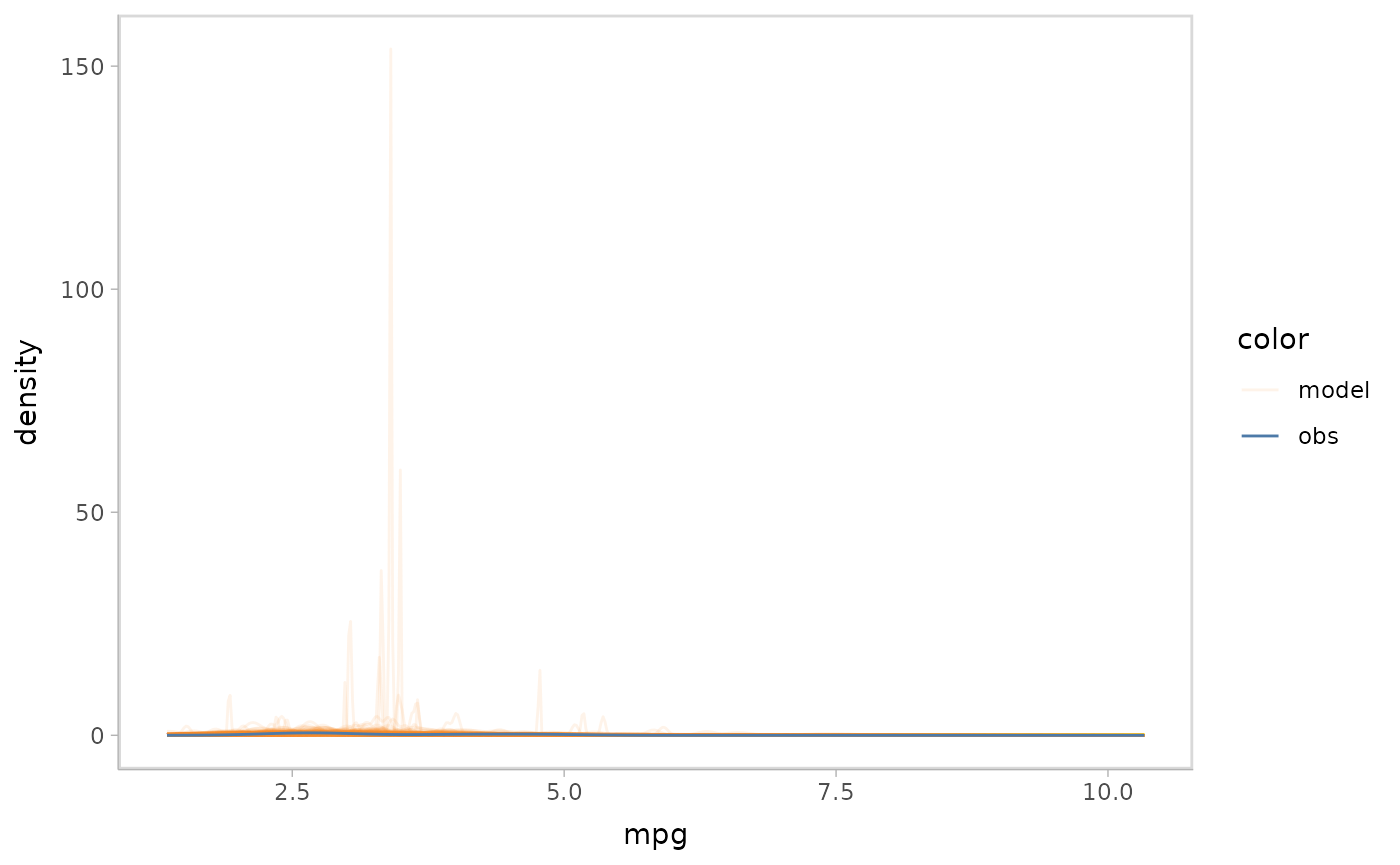

Note that we group the observation by vs and am before transforming by sd() because the model’s sigma has two predictors vs and am. However you can also group them by other variables or even not group them (which will make the observation a single value).

Distributions predicting on new data set

In a model check, we may want to generate the model’s prediction on a new data set, rather than just replicating the output on the data that is used to fit the model. For example, we may want to use modelr::data_grid() to generate a grid describing the predictors we want and then let the model predict on it.

mpg_model %>%
  mcplot() +
  mc_draw("prediction", newdata = data_grid(mpg_model$data, disp, vs, am)) +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.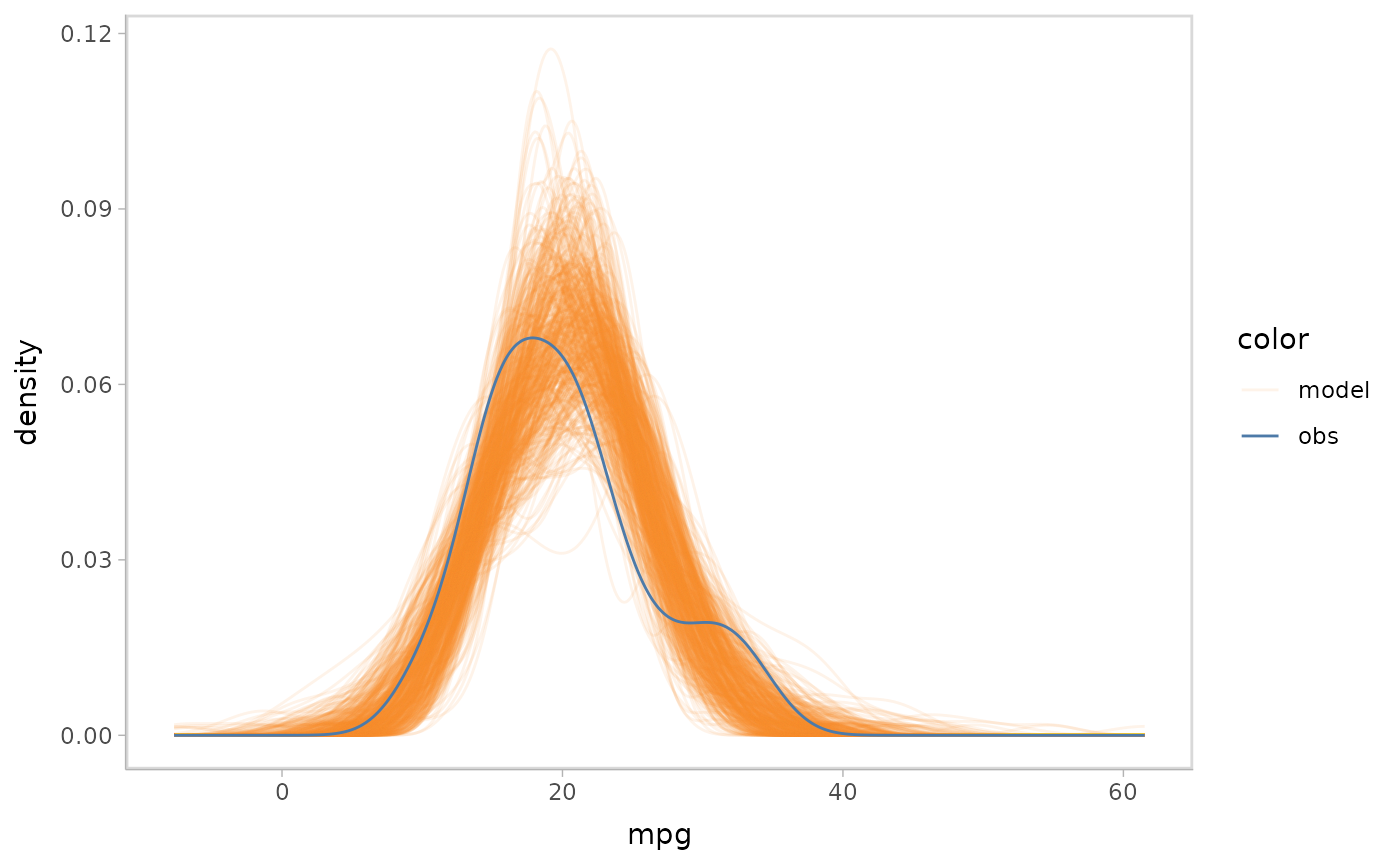

mpg_model %>%
  mcplot() +
  mc_draw("mu", newdata = data_grid(mpg_model$data, disp, vs, am)) +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.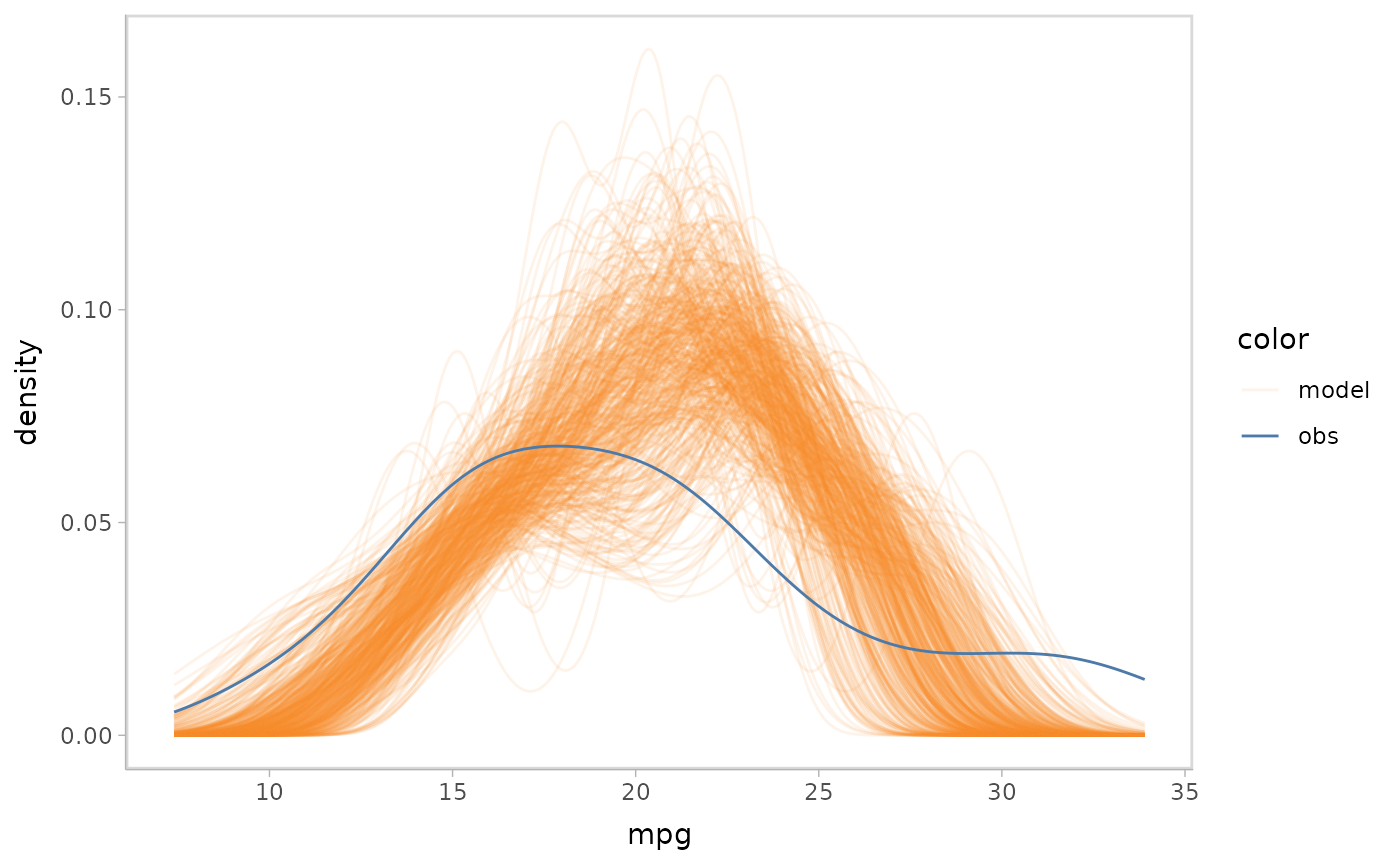

mpg_model %>%
  mcplot() +
  mc_observation_transformation(sd, vars(vs, am)) +
  mc_draw("sigma", newdata = data_grid(mpg_model$data, disp, vs, am)) +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.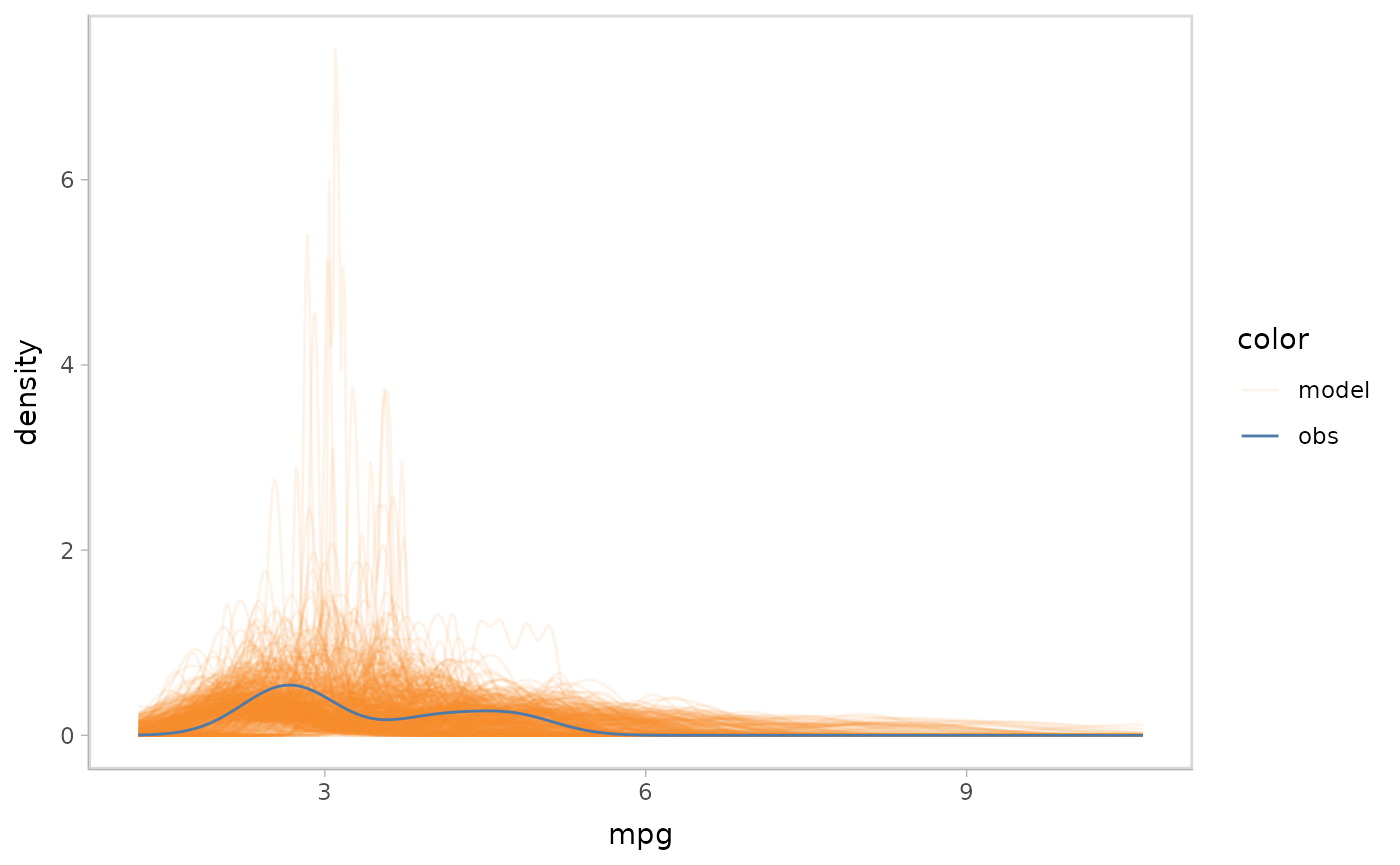

Frequentist models

For the models that are not supported by extract functions in tidybayes, vmc uses insight::get_predicted() to extract the distributions of predictions and push-forward transformations. See a full list of the model types supported by insight by insight::supported_models(). We could choose these to show the predictive distributions, link-scale distributions, and the expectation distribution (the distribution of the expectation of the predictions) when defining mc_draw().

We go through this section to show how to generate model checks using vmc for an example general regression model that is fitted using glm(family = "Gamma") with a push-forward transformation on the inverse scale.

glm_model <- glm(mpg ~ cyl + hp, data = mtcars, family = "Gamma")
glm_model
#> 
#> Call:  glm(formula = mpg ~ cyl + hp, family = "Gamma", data = mtcars)
#> 
#> Coefficients:
#> (Intercept)          cyl           hp  
#>   1.231e-02    4.618e-03    8.331e-05  
#> 
#> Degrees of Freedom: 31 Total (i.e. Null);  29 Residual
#> Null Deviance:       2.735 
#> Residual Deviance: 0.6383    AIC: 162.9

Predictive distribution

Similar to Bayesian models, mcplot() generates a predictive distribution from the model by default if no distribution is specified.

glm_model %>%
  mcplot() +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.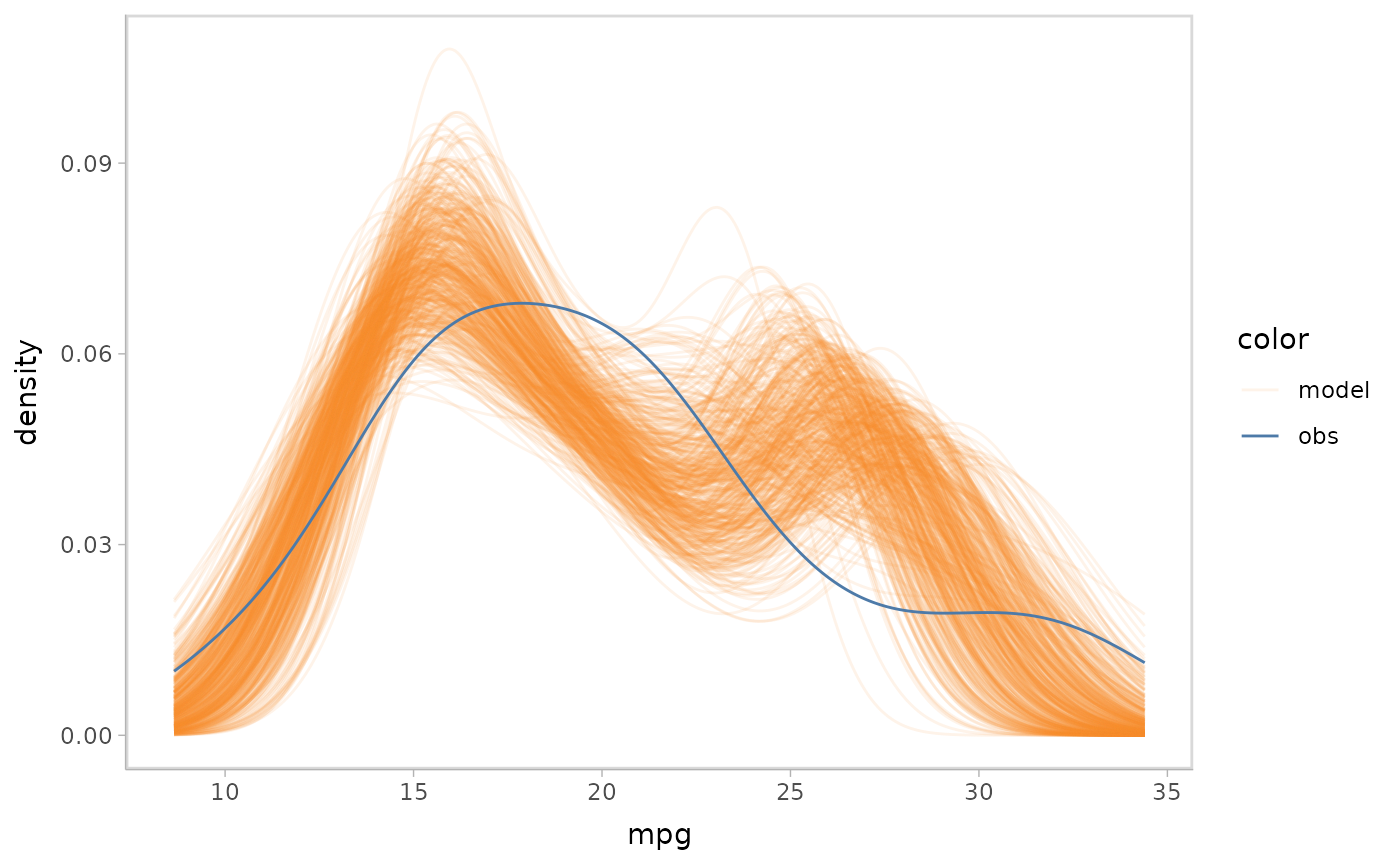

Push-forward transformations

The Gamma family in glm links the response variable using inverse by default. Like the sigma push forward transformation in the example Bayesian model, we could transform the observed data into a scale that is comparable with the inverse link in this model.

glm_model %>% 
  mcplot() +
  mc_observation_transformation(function(x) 1/x) +
  mc_draw("link") +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.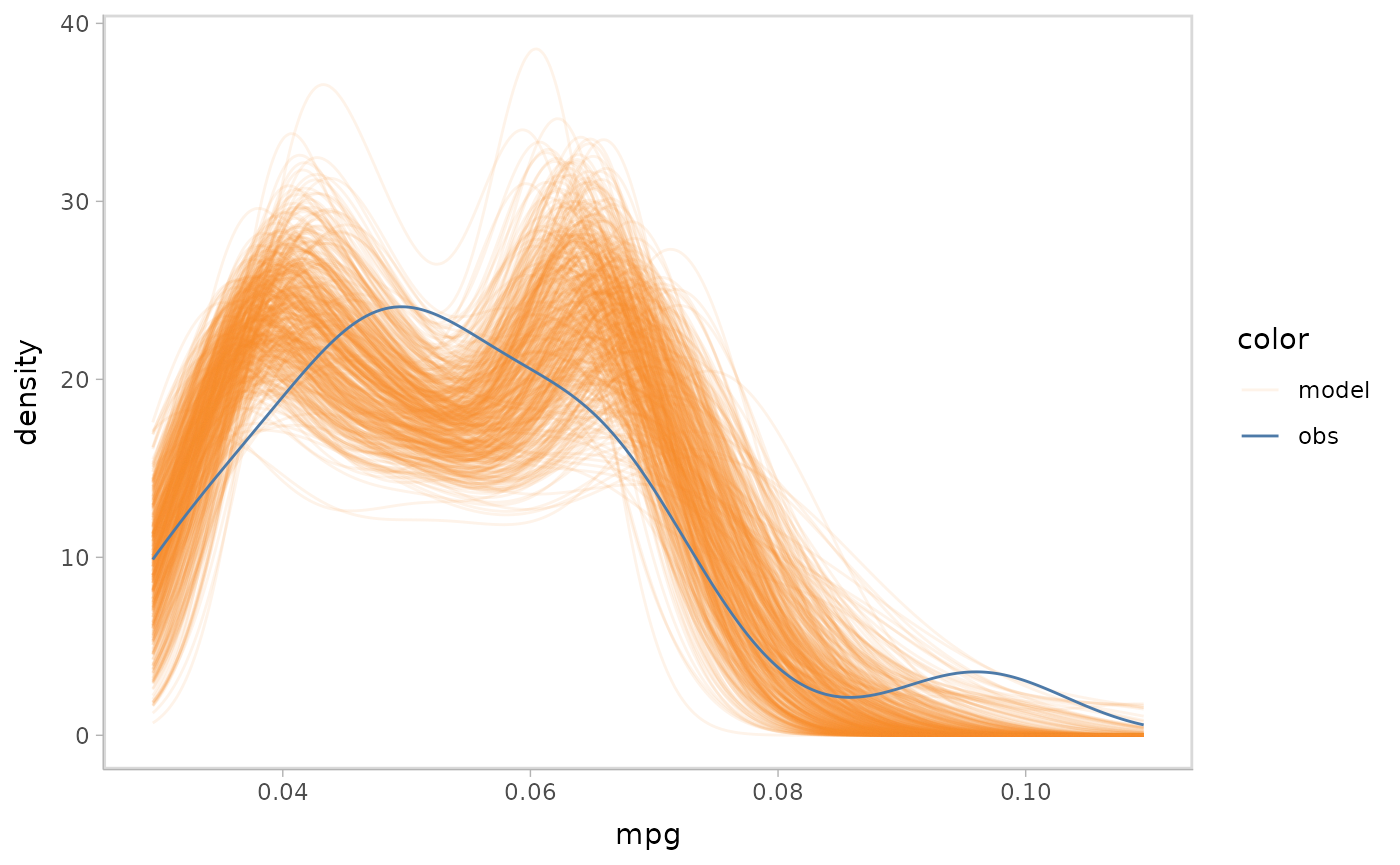

Distributions predicting on new data set

We could also specify a new data set to be used to generate distributions for non-Bayesian models.

glm_model %>%
  mcplot() +
  mc_draw("prediction", newdata = data_grid(get_data(glm_model), cyl, hp)) +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.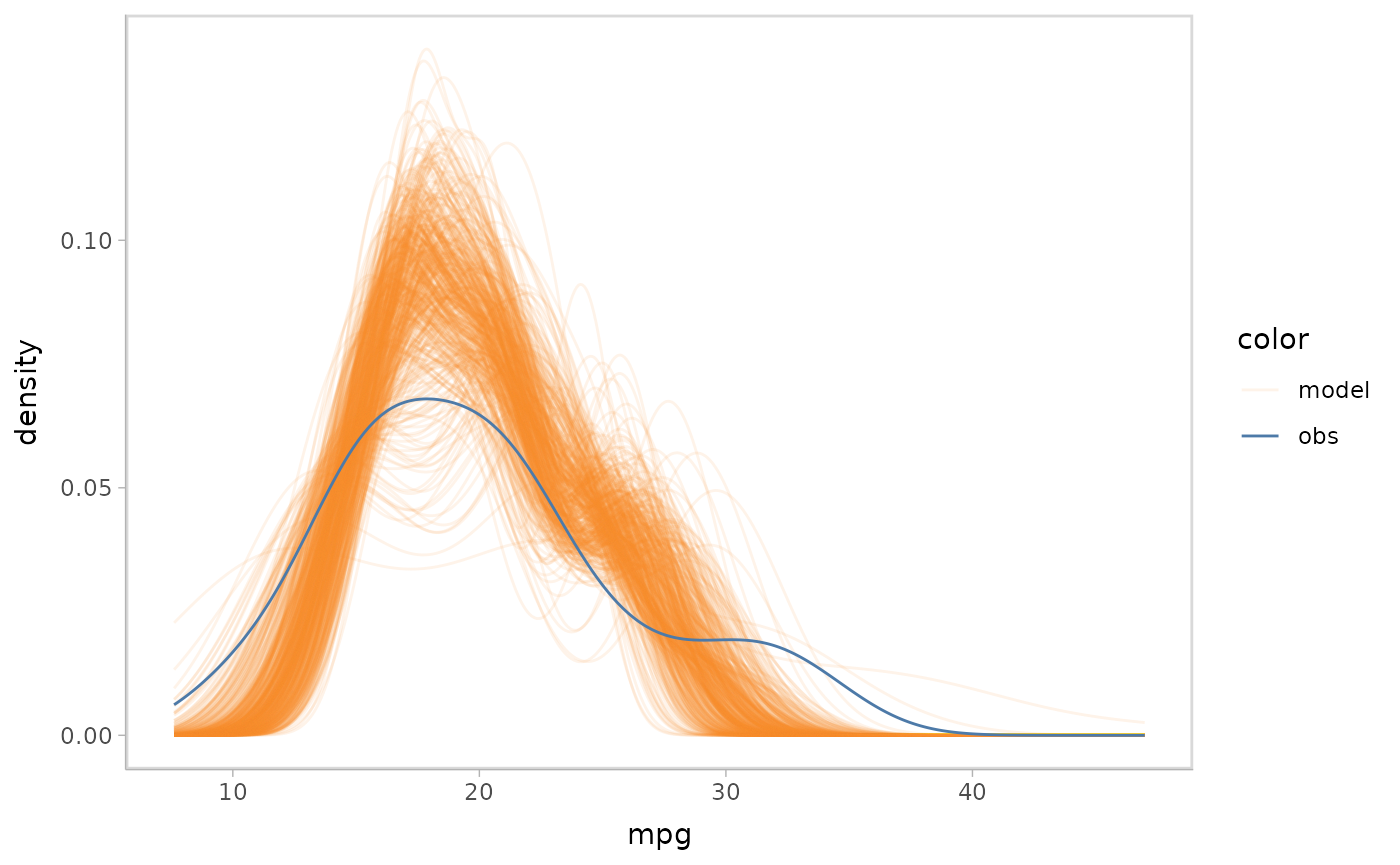

glm_model %>%
  mcplot() +
  mc_observation_transformation(function(x) 1/x) +
  mc_draw("link", newdata = data_grid(get_data(glm_model), cyl, hp)) +
  mc_gglayer(coord_flip())
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's fill values.