Visualizing Uncertainty in Probabilistic Graphs with Network Hypothetical Outcome Plots (NetHOPs)
IEEE Trans. Visualization & Comp. Graphics (Proc. INFOVIS) 2021
At a high level, the NetHOPs creation pipeline starts with formulating a probabilistic random graph model based on a given network dataset. The model provides a network data generating process enabling us to sample a sequence of different network realizations via a Monte Carlo process. We apply our instant-optimal community detection and matching algorithms to the network sequence so each individual realization is supplemented with additional measures that capture community structure across the set. We pass the network sequence to the visualization functions, which compute the layouts and use the additional community structure measures to color communities.
Abstract
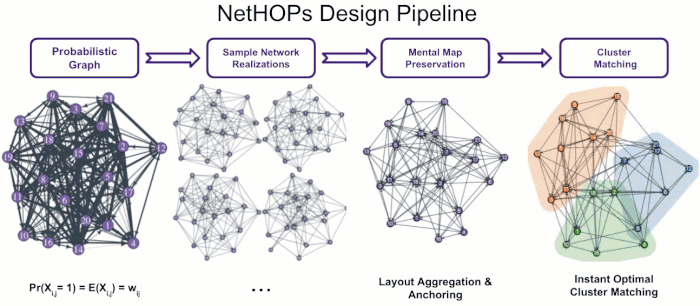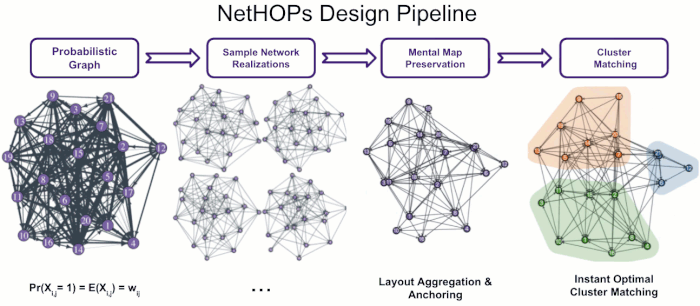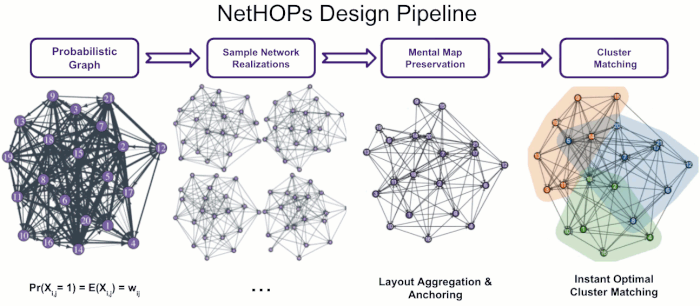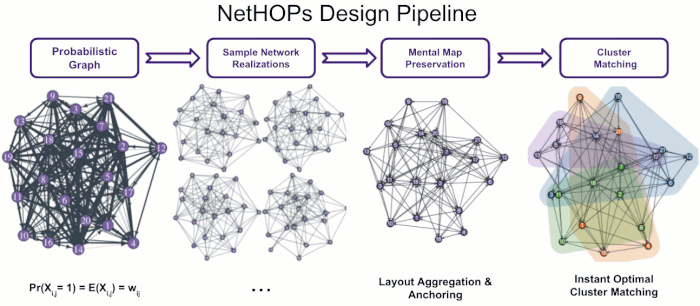
Probabilistic graphs are challenging to visualize using the traditional node-link diagram. Encoding edge probability using visual variables like width or fuzziness makes it difficult for users of static network visualizations to estimate network statistics like densities, isolates, path lengths, or clustering under uncertainty. We introduce Network Hypothetical Outcome Plots (NetHOPs), a visualization technique that animates a sequence of network realizations sampled from a network distribution defined by probabilistic edges. NetHOPs employ an aggregation and anchoring algorithm used in dynamic and longitudinal graph drawing to parameterize layout stability for uncertainty estimation. We present a community matching algorithm to enable visualizing the uncertainty of cluster membership and community occurrence. We describe the results of a study in which 51 network experts used NetHOPs to complete a set of common visual analysis tasks and reported how they perceived network structures and properties subject to uncertainty. Participants’ estimates fell, on average, within 11% of the ground truth statistics, suggesting NetHOPs can be a reasonable approach for enabling network analysts to reason about multiple properties under uncertainty. Participants appeared to articulate the distribution of network statistics slightly more accurately when they could manipulate the layout anchoring and the animation speed. Based on these findings, we synthesize design recommendations for developing and using animated visualizations for probabilistic networks.
Citation
BibTeX
@article{nethops-2021,
title = {Visualizing Uncertainty in Probabilistic Graphs with Network Hypothetical Outcome Plots (NetHOPs)},
author = {Zhang, Dongping and Adar, Eytan and Hullman, Jessica},
year = 2022,
journal = {IEEE Transactions on Visualization and Computer Graphics},
volume = 28,
number = 1,
pages = {443--453},
doi = {10.1109/TVCG.2021.3114679}
}